Statistik und Datenanalyse: Aufbau

Faktorenanalyse

Benjamin Fretwurst
Vollbild PDF-Version

Inhalt

• 1 Messung und Analyse latenter Faktoren
  • 1.1 Multikollinearität und Dimensionsreduktion
  • 1.2 R-Angstskala in unserer Befragung
  • 1.3 Vorgehen der PCA und Faktorenanalyse
  • 1.4 Faktorrotation
• 2 Literaturbeispiel (Übung 3 – siehe LEF)
• Take Home – Ausblick

Orga

Kein Q&A am Donnerstag

Wir holen das die Woche drauf nach. Bis dahin alle Fragen ins Forum!

STP

Es gibt diesen Freitag eine neue Studie für 10 STP!

Statistik-Aufbau PDF so gut es geht

Die PDF-Version des Companion funktioniert mässig, aber besser als nix.

Lernziele

• Sie lernen Explorative Faktorenanalysen kannen.

• Sie können gemessene Variablen auf ihre zugrundeliegenden Faktoren hin untersuchen.

• Sie können stark korrelierte Variablen zusammenfassen, indem Sie deren Faktoren speichern.

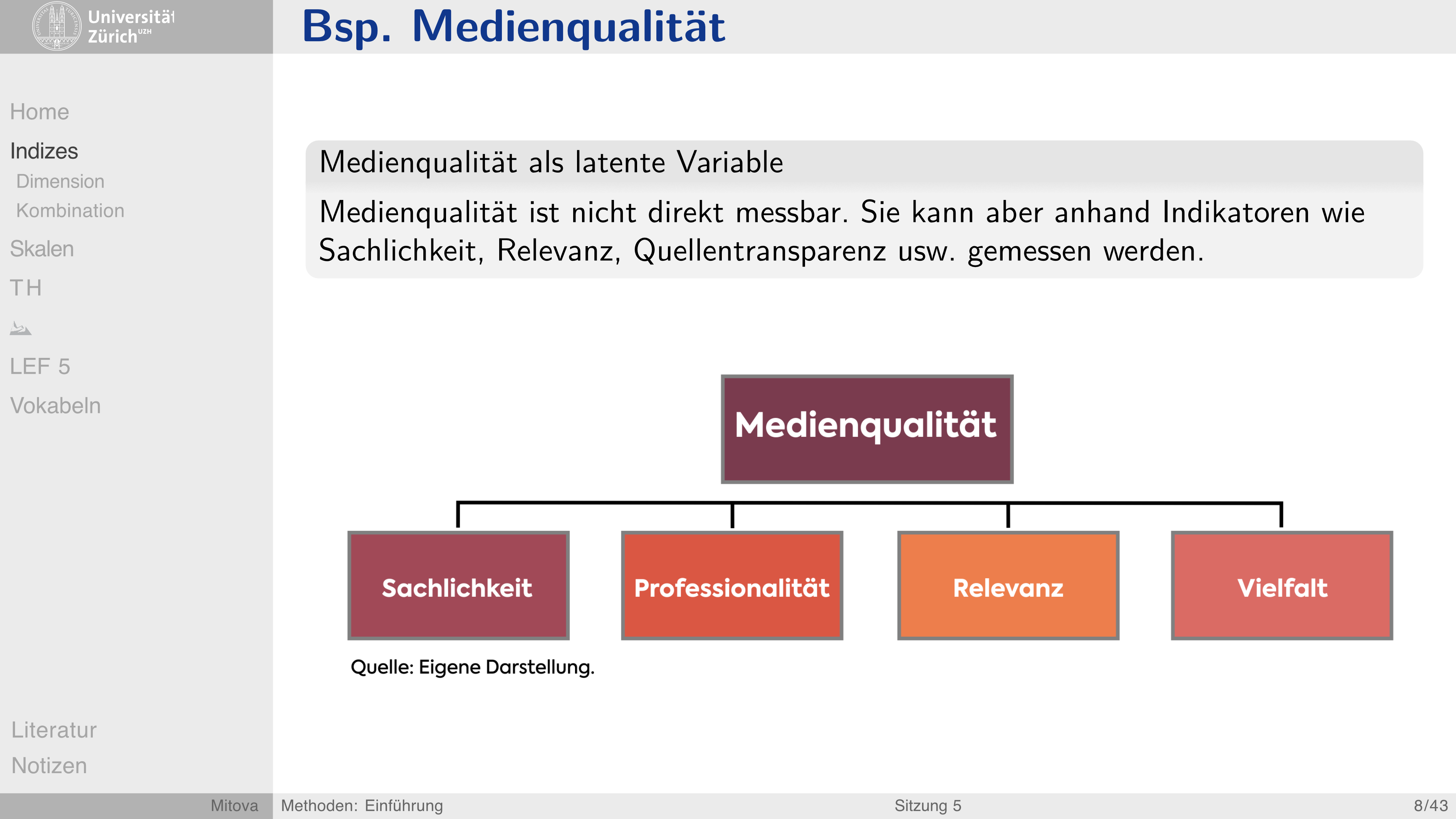
1 Messung und Analyse latenter Faktoren

Was geht? … mit Faktorenanalysen!

• Mit Faktorenanalysen können latente Einflüsse explorativ gefunden werden.
• Die Messung latenter Konstrukte kann (konfirmatorisch) geprüft werden.
• Mit Faktorenanalysen können Indices gebaut werden.
• Wenn UVs in Regressionsmodellen hoch multikollinear sind, können sie zu unkorrelierten Faktoren zusammengefasst werden.

Methoden – Einführung – Indices

Dimensionen

1.1 Multikollinearität und Dimensionsreduktion

Multikollinearität

In einem Koordinationsystem macht jede Variable eine Dimension auf, also 3 Variablen, 3 Achsen → 3D.

Korrelieren die Variablen stark miteinander, liegen sie auf einer Geraden, die nur eine Dimension hat. Man kann die Variablen auf diese eine Dimension reduzieren. Dann müssen wir uns nur noch um eine Variable (Index) «kümmern», statt um drei! Wir versuchen also eine Dimensionsreduktion.

1.2 R-Angstskala in unserer Befragung

Wenn wir mehrere Variablen (zB einer Skala) zu einer reduzieren können, können wir damit Multikollinearitätsprobleme lösen können.

varname	varlabel
R101_07	Computer hassen mich.
R101_12	Leute versuchen dir zu sagen, dass R die Statistik leichter verständlich macht, aber das stimmt nicht.
R101_18	Wenn ich R benutzte, gibt es immer nur Fehlermeldungen.
R101_22	Meine Freunde sind besser in R als ich.
R101_25	Ich arbeite gerne mit R.
R101_27	Die Arbeit mit R stresst und frustriert mich.
R101_29	R verunsichert mich.
R101_30	Das Programm R-Studio fand ich gut.
R101_31	Das Programm R-Studio fand ich unübersichtlich.
R101_32	Mir ist der Unterschied zwischen R und R-Studio klar.

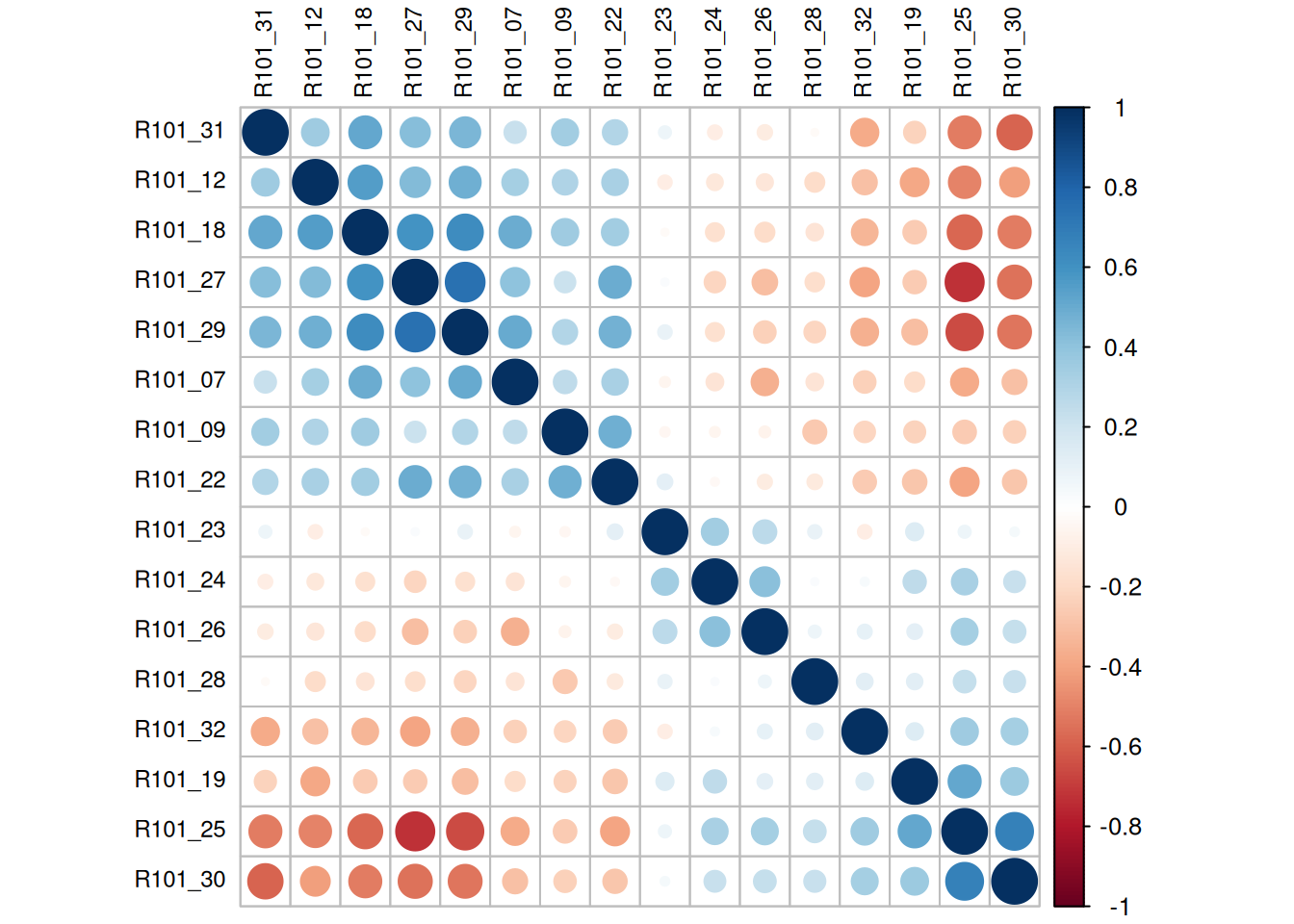
Korrelationsmatrix

• Diagonale 1
• Sortiert nach Korrelation
• Stärke als Kreise und Farbe

Fragen, die die FA beantwortet

Wie viel geht bei der Dimensionsreduktion durch die Faktoren verloren, bzw. was wird abgebildet?

Mit der Gesamtlösung kann man schauen, welchen Anteil der Varianz aller Faktoren durch die Faktorlösung abgebildet wird.

Wie gut werden die Variablen durch die Faktoren abgebildet?

Die Kommunalitäten und «Uniqueness» geben an, wie gut jede Variable durch die gebildeten Faktoren repräsentiert werden.

Was bedeuten die Faktoren?

Faktorladungen geben die Korrelationen der Faktoren mit jeder Variable an. Also welche Faktoren, welche Variablen repräsentieren? Dadurch kann den Faktoren ein Sinn und ein Name gegeben werden.

Faktoren in 3D

• Drei Varialben (3D)
• je mehr n, desto dunkler
• Zwei Faktoren
  • orthogonal
  • unkorreliert
• rotiert

1.3 Vorgehen der PCA und Faktorenanalyse

1. Prüfen, ob ein Set an Variablen für eine Faktorenanalyse geeignet ist

• Korrelationsanalyse

• KMO

2. Feststellen, wie viele latente Faktoren extrahiert werden sollten

• Scree-Plot

• Parallelanalyse

3. Interpretation der Faktoren

• Berechnung der Faktorladungen

• Identifikation der Faktoren (Interpretation)

1.3.1 KMO

Das Kaiser-Meyer-Olkin-Kriterium prüft, ob ein Set von Variablen geeignet ist für eine Faktorenanalyse.

Kommt es nicht gut raus, kann man Variablen mit kleinen Werten ausschliessen.

IYI ∉ Klausur

\text{KMO} = \frac{\sum_{i \neq j} r_{ij}^2}{\sum_{i \neq j} r_{ij}^2 + \sum_{i \neq j} p_{ij}^2}

Kaiser-Meyer-Olkin factor adequacy

• < .5 inakzeptabel
• .50-.59 miserabel
• .60-.69 mässig
• .70-.79 mittel ok
• .80-.89 gut
• .90-1.00 irre super

KMO der RAQ

Der Overall MSA ist 0.896.

tibble::tibble(
  Variable = names(kmo_result$MSAi),
  MSA = kmo_result$MSAi
) |> 
  mutate(Variable = stringr::str_remove(Variable, pattern = "RAQ: "))|>
  mutate(MSA = round(MSA, 2))|>
  gt::gt()|>
  gt::tab_options(table.font.size = 18)

MSA for each item

Variable	MSA
Computer hassen mich.	0.89
Leute versuchen dir zu sagen, dass R die Statistik leichter verständlich macht, aber das stimmt nicht.	0.92
Wenn ich R benutzte, gibt es immer nur Fehlermeldungen.	0.90
Meine Freunde sind besser in R als ich.	0.92
Ich arbeite gerne mit R.	0.90
Die Arbeit mit R stresst und frustriert mich.	0.87
R verunsichert mich.	0.91
Das Programm R-Studio fand ich gut.	0.89
Das Programm R-Studio fand ich unübersichtlich.	0.88
Mir ist der Unterschied zwischen R und R-Studio klar.	0.94

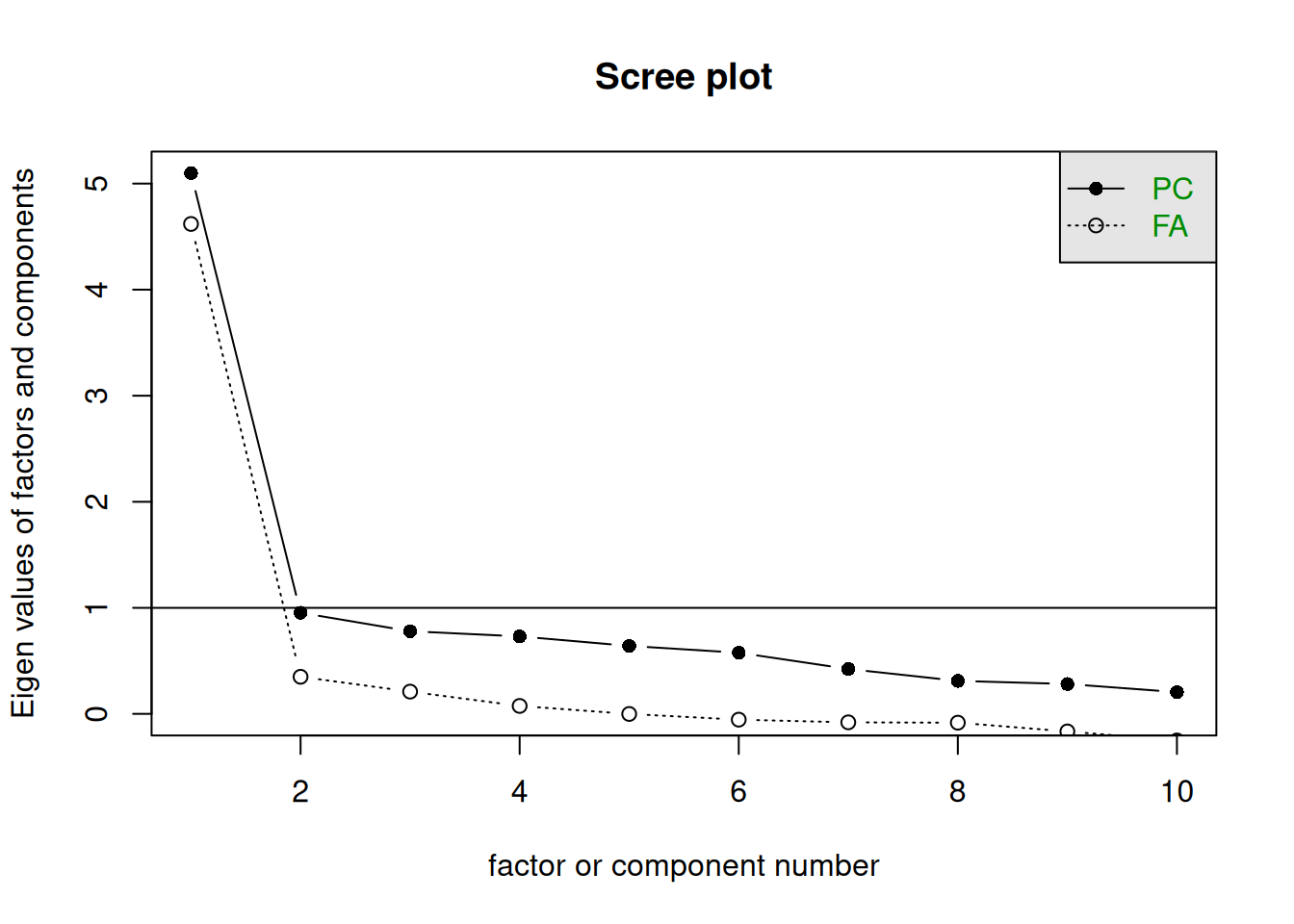
Scree Plot der Eigenwerte (eigen values)

Die «factor number» über der 1-Linie («Eigen values» > 1) ist eine Empfehlung für die Anzahl an Faktoren, bei denen jeder Faktor mehr Varianz (Eigenwert > 1) auf sich vereint als die ursprünglichen Dimensionen.

raq_items  <- scale(raq_items_tib)

raq_items |>
  psych::scree(pc = TRUE)

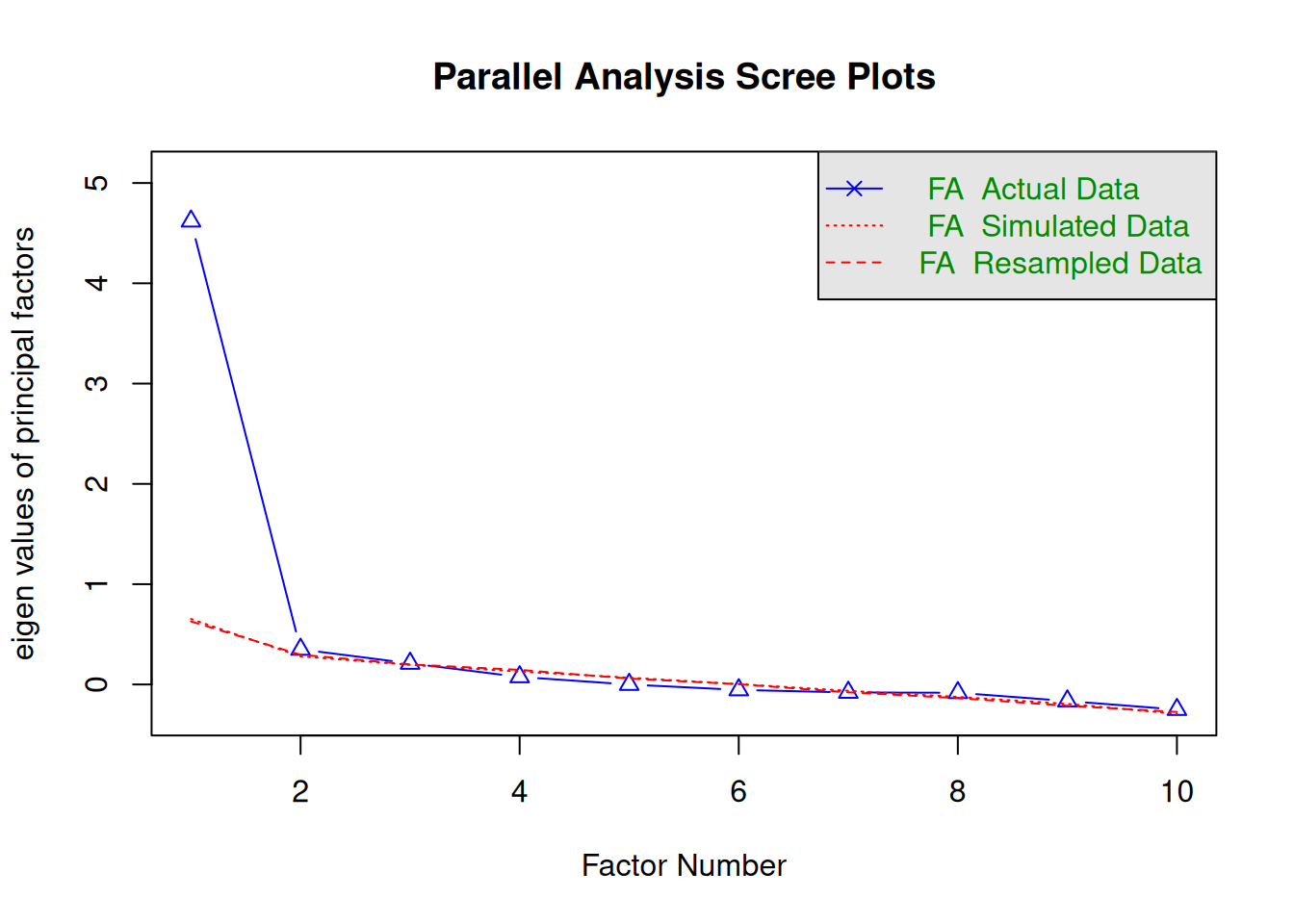
1.3.2 Parallel Analysis als Alternative zum Scree Plot

Wie viele Faktoren soll es geben? Wie viele haben einen “Eigenvalue” > 1?

raq_items |>
 psych::fa.parallel(fa = "fa")

Parallel analysis suggests that the number of factors = 2 and the number of components = NA

1.3.3 Skalenreliabilität der Faktoren (Cronbachs \alpha)

Skalenreliabilität

Skalenreliabilität ist die innere Konsistenz einer Skala. Der gängigste Koeffizient für die Skalenrelaiblität ist Cronbachs \alpha. Er geht von -\infty bis 1, wobei 1 wäre perfekt.

\begin{align*} \alpha_{st} &= \frac{K \cdot \overline{r}}{1+(K-1) \cdot \overline{r}} \end{align*}

\alpha_{st}: standardisiertes Cronbach \alpha
K: Anzahl Elemente (Variablen) einer Skala
\overline{r}: Durchschnittliche Korrelation

1.4 Faktorrotation

Unrotiert

Beim Verfahren der Faktorenanalyse wird erst ein Faktor in die Variablen gelegt, der alle am besten erklärt. Dann kommt der zweite und optimiert den Rest der Varianz usw. Das ergibt ein Ungleichgewicht zwischen den Faktoren. Darum wird rotiert.

Orthogonale und oblique Rotation

Faktoren werden rotiert, damit jeder optimal Varianz erklärt. Wenn orthogonal rotiert wird, sind die Faktoren 100% unkorreliert. Nach obliquer Rotation sind die Faktoren leicht korreliert, geben aber die Variablen besser wieder.

Faktorrotation

Bei orthogonaler Rotation sind die Faktoren unkorreliert.
Orthogonal ist klarer interpretierbar …

Bei der obliquen dürfen sie leicht korrelieren.
… oblique gibt realistischere Ergebnisse.

1.4.1 Faktorladungen

• Faktorladungen sind die Korrelationen der Variablen mit den Faktoren
• Faktorladungen geben an, wie stark jeder Faktor mit den einzelnen Variablen zusammenhängt bzw. wie stark er sie bestimmt.
• Jeder Faktor wird anhand der Variablen mit den höchsten Ladungen auf diesem Faktor interpretiert.

1.4.2 Faktorladungen RAQ

Faktorladungen

Variable	MR1	MR3	MR2	Complexity	Uniqueness
RAQ: Die Arbeit mit R stresst und frustriert mich.	0.90	—	—	1.01	0.18
RAQ: R verunsichert mich.	0.65	0.26	—	1.30	0.27
RAQ: Meine Freunde sind besser in R als ich.	0.51	—	—	1.20	0.69
RAQ: Ich arbeite gerne mit R.	-0.49	—	0.42	1.96	0.30
RAQ: Wenn ich R benutzte, gibt es immer nur Fehlermeldungen.	—	0.78	—	1.06	0.25
RAQ: Computer hassen mich.	0.25	0.52	—	1.73	0.62
RAQ: Leute versuchen dir zu sagen, dass R die Statistik leichter verständlich macht, aber das stimmt nicht.	—	0.46	—	1.30	0.60
RAQ: Das Programm R-Studio fand ich gut.	—	—	0.75	1.04	0.30
RAQ: Das Programm R-Studio fand ich unübersichtlich.	—	—	-0.62	1.21	0.49
RAQ: Mir ist der Unterschied zwischen R und R-Studio klar.	—	—	0.22	2.60	0.78

1.4.3 Variableneignung – Kommunalitäten & Uniqueness

Kommunalitäten

Die Kommunalität einer Variable ist der Varianzanteil, den sie mit den extrahierten Faktoren teilt. Kommunalitäten unter .4 sind eher dürftig.

Uniqueness = 1 - Kommunalität

Die Uniqueness-Werte drücken aus, wie hoch der Varianzanteil ist, der nicht durch die Faktorenlösung erklärt werden konnte. Werte über .6 sind eher dürftig.

Complexity

Die Komplexität je Variable gibt an, ob es Mehrfachladungen auf einer Variable gibt. Wenn sie 1 ist, dann ist das Ergebnis eindeutig, wenn sie nahe 2 ist, dann laden zwei Faktoren auf dieser Variable.

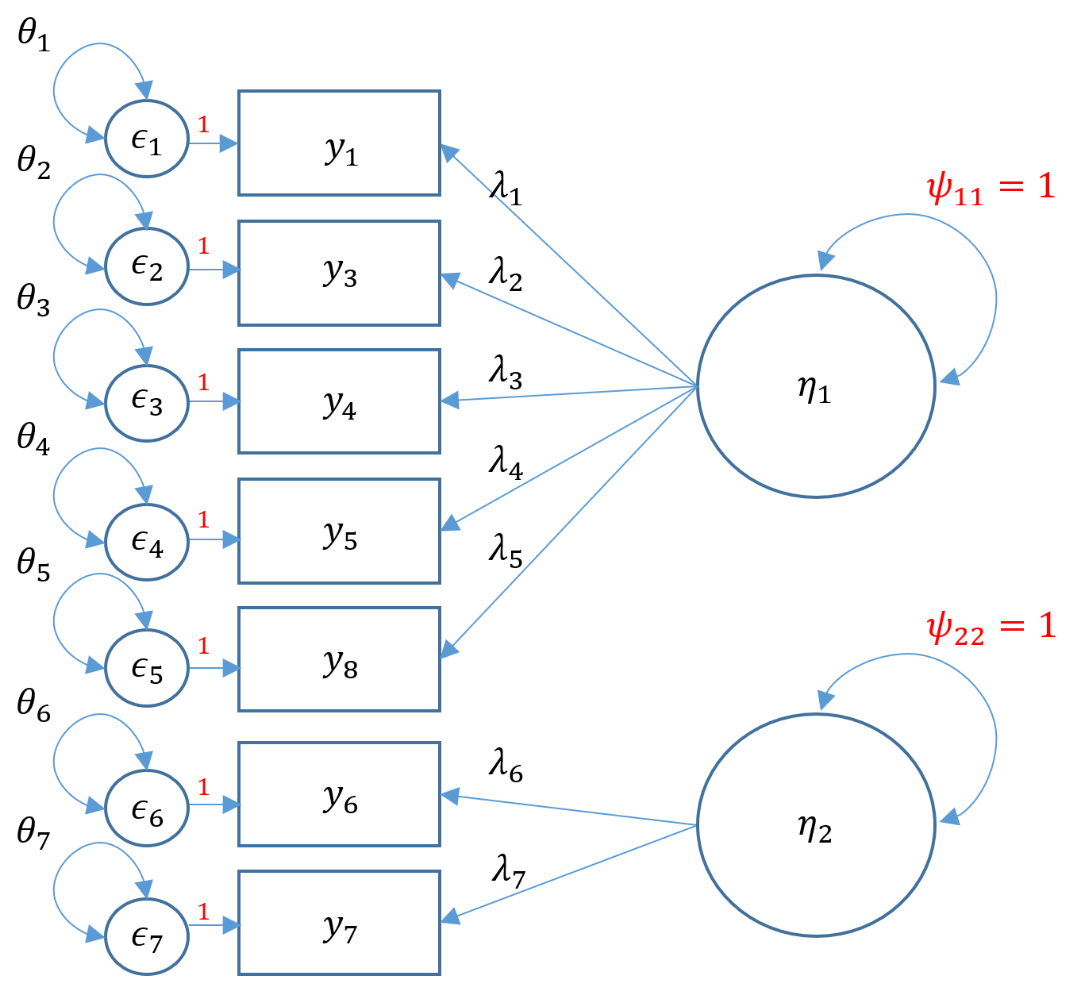
1.4.4 FA als SEM – is future music

Mit der konfirmatorischen FA (CFA) werden angenommene Faktoren geprüft!

Konfirmatorische Faktorenanalyse mit Strukturgleichungsmodell (SEM)

2 Literaturbeispiel (Übung 3 – siehe LEF)

EFA Song et al. (2004)

Take Home – Ausblick

Take Home

Faktorenanalyse

Sie wissen, wie man Konstrukte (Faktoren) durch mehrere, hoch korrelierte, metrische Variablen, also Skalen erfasst.

Sie können eine explorative Faktorenanalyse durchführen und interpretieren.

Ausblick

Übung Faktorenanalyse

Wir schauen uns an, wie man bei Multikollinearität (zB in NF) Indices bauen kann (Mittelwert oder Summenindex) oder wie man das Problem mit der Faktorenanalyse in den Griff kriegen kann.

Song, Indeok, Robert Larose, Matthew S. Eastin, and Carolyn A. Lin. 2004. “Internet Gratifications and Internet Addiction: On the Uses and Abuses of New Media.” CyberPsychology & Behavior 7 (4): 384–94. https://doi.org/10.1089/cpb.2004.7.384.